Mitch Richling: Tinkerbell Fractal

Author:	Mitch Richling
Updated:	2024-09-07

1. Introduction
2. Algorithms
3. Gallery
4. References

1. Introduction

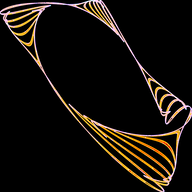
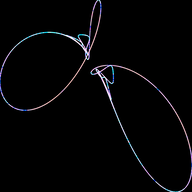
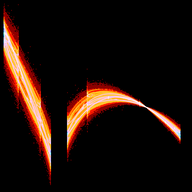
The Tinkerbell Attractor is a discrete-time dynamical system defined by the following relationship: \[ \begin{align*} x_{n+1} & = x_n^2-y_n^2+ax_n+by_n \\ y_{n+1} & = 2x_ny_n+cx_n+dy_n \end{align*} \] Most any non-zero initial conditions may be used for \( (x_1, y_1) \).

2. Algorithms

Just as with the Peter de Jong attractors we look at the probability density function, \(P(x,y)\), defined by the probability that some \((x_n, y_n)\) from the map will be in a neighborhood of \((x,y)\). While that sounds complicated, producing a visualization of this PDF is quite simple in practice – we simply visualize a histogram based on computed values of the map. The first step is to define a rectangular region of the plane over which we wish to visualize the PDF, and then define a set of discrete pixels over that region. Then we compute a few million, or billion, iterations of the map, and count the number of times we hit each pixel.

#include "ramCanvas.hpp"

std::vector<std::array<double, 11>> params {
  /*        a,         b,          c,         d,  x0,  y0,   N,     x-min,    x-max,     y-min,     y-max */
  {  0.900000, -0.220000,  2.0000000,  0.500000, 0.1, 0.1, 1e7, -1.410000, 0.370000, -1.380000, -0.350000 }, //   0
  {  0.200000,  0.150000,  2.0000000,  0.650000, 0.1, 0.1, 1e7, -1.460000, 0.950000, -1.240000, -0.150000 }, //   1
  {  0.900000, -0.601300,  2.0000000,  0.500000, 0.1, 0.1, 1e7, -1.240000, 0.470000, -1.560000,  0.550000 }, //   2
  { -0.783671, -0.450251,  0.0756921,  1.908150, 0.1, 0.1, 1e8, -0.784949, 0.190357,  0.100000,  1.012020 }, //   3
  { -0.667316,  0.789788,  1.1057300,  0.268078, 0.1, 0.1, 1e8, -0.903469, 1.087990, -0.708937,  0.319083 }, //   4
  { -1.016430, -1.458560,  1.3230100,  0.604218, 0.1, 0.1, 1e8, -0.399636, 0.403479, -0.562466,  0.225223 }, //   5
  { -0.254258,  0.925243,  0.7704410, -0.416270, 0.1, 0.1, 1e8, -0.888853, 0.939351, -0.734047,  0.346012 }, //   6
  { -1.548590, -0.249840, -0.2864630,  1.508330, 0.1, 0.1, 1e8, -0.849159, 1.357350, -0.054140,  1.033830 }, //   7
  { -0.769882, -0.743097, -1.0527500,  0.216079, 0.1, 0.1, 1e8, -0.864322, 1.141670, -0.394488,  0.686611 }, //   8
  { -0.305249, -0.507228, -1.5821000,  0.919462, 0.1, 0.1, 1e8, -1.234830, 0.745791,  0.300000,  0.881405 }, //   9
  { -1.754900, -0.904038,  0.9181340,  1.379920, 0.1, 0.1, 1e8, -0.821663, 1.448790, -2.112250, -0.100000 }, //  10
  { -1.659840, -1.286440,  0.7102750,  1.097500, 0.1, 0.1, 1e8, -0.412856, 0.803154, -1.709030, -0.800778 }, //  11
  { -1.733520, -0.647135,  0.5964760,  0.988405, 0.1, 0.1, 1e8, -0.700000, 1.800000, -0.312000, -0.273000 }, //  12
};

int main(void) {
  std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now();
  const int BSIZ = 480*8;
  mjr::ramCanvas1c16b::colorType aColor;
  aColor.setChans(1);

  for(decltype(params.size()) j=0; j<params.size(); ++j) {
    mjr::ramCanvas1c16b theRamCanvas(BSIZ, BSIZ, params[j][7], params[j][8], params[j][9], params[j][10]);

    double a = params[j][0];
    double b = params[j][1];
    double c = params[j][2];
    double d = params[j][3];

    /* Draw the Attractor on a 16-bit, greyscale canvas such that the level is the hit count for that pixel.  
       Thus we are using an "image" as a way to store field data instead of color information. */
    double x        = params[j][4];
    double y        = params[j][5];
    uint64_t maxII  = 0;
    uint64_t inCnt  = 0;
    uint64_t maxItr = static_cast<uint64_t>(params[j][6]);
    uint64_t iPrt   = maxItr / 5;
    uint64_t itr;
    for(itr=1;itr<maxItr;itr++) {
      double xNew = x*x-y*y+a*x+b*y;
      double yNew = 2*x*y+c*x+d*y;
      if ( !theRamCanvas.isCliped(x, y)) {
        inCnt++;
        theRamCanvas.drawPoint(x, y, theRamCanvas.getPxColor(x, y).tfrmAdd(aColor));
        if(theRamCanvas.getPxColor(x, y).getC0() > maxII) {
          maxII = theRamCanvas.getPxColor(x, y).getC0();
          if(maxII > 16384) { // 1/4 of max possible intensity
            std::cout << "ITER(" << j <<  "): " << itr << " MAXS: " << maxII << " EXIT: Maximum intensity reached" << std::endl;
            break;
          }
        }
      }
      if((itr % iPrt) == 0)
        std::cout << "ITER(" << j <<  "): " << itr << " MAXS: " << maxII << " INC: " << inCnt << std::endl;
      x=xNew;
      y=yNew;
    }
    std::cout << "ITER(" << j <<  "): " << itr << " MAXS: " << maxII << " INC: " << inCnt  << std::endl;

    // Log image transform
    theRamCanvas.applyHomoPixTfrm(&mjr::ramCanvas1c16b::colorType::tfrmLn1);
    maxII = static_cast<uint64_t>(std::log(static_cast<double>(maxII)));

    /* Create a new image based on csCCfractal0RYBCW -- this one is 24-bit RGB color. */
    mjr::ramCanvas3c8b anotherRamCanvas(BSIZ, BSIZ);
    typedef mjr::ramCanvas3c8b::colorType::csCCfractal0RYBCW cs_t;
    for(int yi=0;yi<theRamCanvas.getNumPixY();yi++)
      for(int xi=0;xi<theRamCanvas.getNumPixX();xi++)
        anotherRamCanvas.drawPoint(xi, yi, cs_t::c(theRamCanvas.getPxColor(xi, yi).getC0() / static_cast<mjr::ramCanvas3c8b::csFltType>(maxII)));

    anotherRamCanvas.writeTIFFfile("tinkerbell_" + mjr::fmtInt(j, 2, '0') + ".tiff");
  }
  std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime;
  std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl;
  return 0;
}