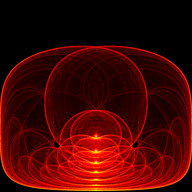
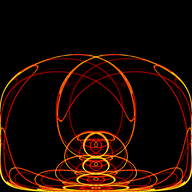
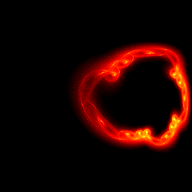
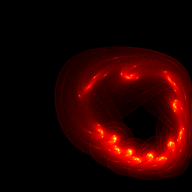
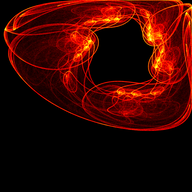
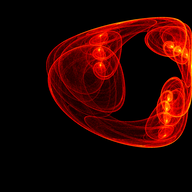
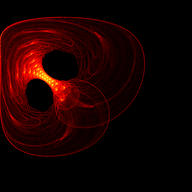
Mitch Richling: The Simone Attractor
| Author: | Mitch Richling |
| Updated: | 2025-02-25 |
Table of Contents
1. Introduction
I came across the Simone Attractor on Paul Bourke's web site (http://www.paulbourke.net/fractals/simone_orbits/). Apparently it's based on, or inspired by, work done by Simone Conradi; however, the web page provides no references. The governing iteration is as follows:
\[ \begin{eqnarray} x_{n+1} & = & \sin(x^2_n - y^2_n+a) \\ y_{n+1} & = & \cos(2 x_n y_n+b) \\ \end{eqnarray} \]
2. Making Images
#include "ramCanvas.hpp" #include "MRMathSTR.hpp" std::vector<std::array<mjr::ramCanvas1c16b::coordFltType, 5>> params { /* a b maxitr */ { 0.432882, -1.570796, 10000000}, // 00 { 0.536566, 1.570796, 10000000}, // 01 { 0.690363, 0.995086, 10000000}, // 02 { 0.517835, 1.680190, 10000000}, // 03 { 0.565480, 1.062950, 10000000}, // 04 { 0.546562, 1.135860, 10000000}, // 05 { 0.456968, 1.837620, 10000000}, // 06 { 0.484075, 1.234150, 10000000}, // 07 { 0.491253, 1.127530, 10000000}, // 08 { 0.443006, 1.747070, 10000000}, // 09 { 0.490425, 1.223740, 10000000}, // 10 { 0.464411, 1.909230, 10000000}, // 11 { 0.486090, 1.139340, 10000000}, // 12 { 0.448678, 1.075730, 10000000}, // 13 { 0.465456, 1.154130, 10000000}, // 14 { 0.375753, 1.877880, 10000000}, // 15 { 0.351747, 1.345850, 10000000}, // 16 { 0.375383, 1.495300, 10000000}, // 17 { 0.378139, 1.323700, 10000000}, // 18 { 0.407792, 1.786880, 10000000}, // 19 { 0.381058, 1.749780, 10000000}, // 20 { 0.422341, 1.361320, 10000000}, // 21 { 0.720252, -1.100380, 10000000}, // 22 { 0.382110, -1.012590, 10000000}, // 23 { 0.404479, -1.626160, 10000000}, // 24 { 0.442941, -1.453160, 10000000}, // 25 { 0.458452, -1.380980, 10000000}, // 26 { 0.064952, -0.775113, 10000000}, // 27 { -0.068023, -0.802403, 10000000}, // 28 { 0.254331, -0.762604, 10000000}, // 29 { -0.223881, -0.714717, 10000000}, // 30 { -0.537199, -0.809482, 10000000}, // 31 { -0.528728, -0.864537, 10000000}, // 32 { -0.783708, -1.135120, 10000000}, // 33 { -0.629771, -0.964981, 10000000}, // 34 { -0.557026, -0.844882, 10000000}, // 35 { -0.501792, -0.675246, 10000000}, // 36 { 0.032832, -0.709609, 10000000}, // 37 { 0.519031, -1.436470, 10000000}, // 38 { 0.037161, 1.936070, 10000000}, // 39 }; int main(void) { std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now(); const int BSIZ = 7680/1; # pragma omp parallel for schedule(static,1) for(decltype(params.size()) j=0; j<params.size(); ++j) { mjr::ramCanvas1c16b theRamCanvas(BSIZ, BSIZ, -1.0, 1.0, -1.0, 1.0); decltype(theRamCanvas)::coordFltType a = params[j][0]; decltype(theRamCanvas)::coordFltType b = params[j][1]; uint64_t maxitr = static_cast<uint64_t>(params[j][2]); decltype(theRamCanvas)::coordFltType xn = 0; decltype(theRamCanvas)::coordFltType yn = 0; for(uint64_t i=0;i<maxitr;i++) { decltype(theRamCanvas)::coordFltType tmp = std::sin(xn*xn-yn*yn+a); yn = std::cos(2*xn*yn+b); xn = tmp; if(i>1000) { decltype(theRamCanvas)::coordIntType ix = theRamCanvas.real2intX(xn); decltype(theRamCanvas)::coordIntType iy = theRamCanvas.real2intY(yn); if (theRamCanvas.isOnCanvas(ix, iy)) theRamCanvas.getPxColorRefNC(ix, iy).tfrmAdd(1); } if((i % 10000000) == 0) # pragma omp critical std::cout << "ITER(" << j << "): " << i << std::endl; } theRamCanvas.autoHistStrech(); theRamCanvas.applyHomoPixTfrm(&decltype(theRamCanvas)::colorType::tfrmPow, 1/4.0); theRamCanvas.rotate90CW(); theRamCanvas.scaleDownMean(4); theRamCanvas.autoHistStrech(); # pragma omp critical std::cout << "ITER(" << j << "): " << "DONE" << std::endl; theRamCanvas.writeTIFFfile("simone_attractor_" + mjr::math::str::fmt_int(j, 2, '0') + ".tiff", mjr::ramCanvasPixelFilter::ColorSchemeOnChan<decltype(theRamCanvas), mjr::color3c8b, mjr::color3c8b::csCColdeFireRamp>(theRamCanvas)); } std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime; std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl; return 0; }
Source Link: simone_attractor.cpp
4. Making Movies
We can animate this attractor by making one or more of the parameters sweep a range of values. The following code illustrates one way to do just that.
#include "ramCanvas.hpp" #include "MRMathSTR.hpp" int main(void) { std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now(); const int BSIZ = 6400; const int NUMFRM = 15*6; const double R = 0.002; const double ANGMIN = 0.0; const double ANGMAX = std::numbers::pi*2; const uint64_t MAXITR = 10000000; # pragma omp parallel for schedule(static,1) for(int frame=0; frame<NUMFRM; frame++) { mjr::ramCanvas1c16b theRamCanvas(BSIZ, BSIZ, -0.6, 0.6, -0.25, 1.0); decltype(theRamCanvas)::coordFltType angle = frame*(ANGMAX-ANGMIN)/NUMFRM+ANGMIN; decltype(theRamCanvas)::coordFltType a = 0.382110 + R * std::cos(angle); decltype(theRamCanvas)::coordFltType b = -1.012590 + R * std::sin(angle); decltype(theRamCanvas)::coordFltType xn = 0; decltype(theRamCanvas)::coordFltType yn = 0; for(uint64_t i=0;i<MAXITR;i++) { decltype(theRamCanvas)::coordFltType tmp = std::sin(xn*xn-yn*yn+a); yn = std::cos(2*xn*yn+b); xn = tmp; if(i>1000) { decltype(theRamCanvas)::coordIntType ix = theRamCanvas.real2intX(xn); decltype(theRamCanvas)::coordIntType iy = theRamCanvas.real2intY(yn); if (theRamCanvas.isOnCanvas(ix, iy)) theRamCanvas.getPxColorRefNC(ix, iy).tfrmAdd(1); } } theRamCanvas.autoHistStrech(); theRamCanvas.applyHomoPixTfrm(&decltype(theRamCanvas)::colorType::tfrmPow, 1/4.0); theRamCanvas.rotate90CW(); theRamCanvas.scaleDownMean(8); theRamCanvas.autoHistStrech(); # pragma omp critical std::cout << "FRAME(" << frame << "): DONE" << std::endl; theRamCanvas.writeTIFFfile("simone_attractor_bmovie_" + mjr::math::str::fmt_int(frame, 4, '0') + ".tiff", mjr::ramCanvasPixelFilter::ColorSchemeOnChan<decltype(theRamCanvas), mjr::color3c8b, mjr::color3c8b::csCColdeFireRamp>(theRamCanvas)); } std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime; std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl; return 0; }
Source Link: simone_attractor_bmovie.cpp