Jump to my Home Page Send me a message Check out stuff on GitHub Check out my photography on Instagram Check out my profile on LinkedIn Check out my profile on reddit Check me out on Facebook

Mitch Richling: Phoenix Fractal

Author: Mitch Richling
Updated: 2024-10-24

phoenix_00_2.png phoenix_04_2.png phoenix_01_2.png

Table of Contents

1. Introduction

The Phoenix Fractal is given by the following iteration:

\[ z_n = z_{n-1} + c + p\cdot z_{n-1} \]

Where \( c \) and \( p \) are both complex parameters we may set as we wish.

This formula is iterated for each point in the complex plane (z) with the initial conditions:

\[ \begin{align*} z_{-1} & = \Im(z) + \Re(z)\cdot i \\ z_{-2} & = 0 \end{align*} \]

An exterior distance estimator is given by:

\[ d_{n} = 2\cdot d_{n-1}\cdot z_{n-1} + p\cdot d_{n-2} \]

With the initial conditions:

\[ \begin{align*} d_{-1} & = 1 \\ d_{-2} & = 0 \end{align*} \]

2. Static Image: Escape Time

These fractals are generated in the same manner as Mandelbrot Julia Sets.

2.1. Code

#include "ramCanvas.hpp"

typedef mjr::ramCanvas3c8b::colorType ct;

std::vector<std::array<double, 9>> params {
  /*       cr,       ci,       pr,       pi,    k, x-min, x-max, y-min, y-max */
  {  0.566700,  0.00000, -0.50000,  0.00000, 10.0, -1.35,  1.35, -1.35,  1.35}, //  0 
  {  0.544992,  0.00000, -0.47000,  0.00000, 10.0, -1.35,  1.35, -1.35,  1.35}, //  1
  {  0.269000,  0.00000,  0.00000,  0.01000,  5.0, -1.10,  1.10, -1.00,  1.00}, //  2
  { -0.400000,  0.10000,  0.29550,  0.00000, 10.0, -1.10,  1.10, -1.50,  1.50}, //  3
  {  0.400000,  0.00000, -0.25000,  0.00000, 10.0, -1.30,  1.20, -1.00,  1.00}, //  4
  {  0.100000,  0.60000, -0.35000,  0.00000, 10.0, -1.30,  1.30, -1.30,  1.30}, //  5
  {  0.400000,  0.40000,  0.20500,  0.00000, 30.0, -1.30,  1.30, -1.30,  1.30}, //  6
  {  0.400000,  0.50000,  0.20500,  0.00000, 30.0, -1.30,  1.30, -1.30,  1.30}, //  7
};

int main(void) {
  std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now();
  const int    WIDTH  = 1920*4;
  const int    HEIGHT = 1920*4;
  const int    NUMITR = 500;
  const double MAXZ   = 4.0;

# pragma omp parallel for schedule(static,1)
  for(decltype(params.size()) j=0; j<params.size(); ++j) {
    const std::complex<double> c(params[j][0], params[j][1]);
    const std::complex<double> p(params[j][2], params[j][3]);
    mjr::ramCanvas3c8b theRamCanvas(WIDTH, HEIGHT, params[j][5], params[j][6], params[j][7], params[j][8]);
    for(int y=0;y<theRamCanvas.getNumPixY();y++) {
      for(int x=0;x<theRamCanvas.getNumPixX();x++) {
        std::complex<double> z1(theRamCanvas.int2realY(y), theRamCanvas.int2realX(x));
        std::complex<double> z2(0.0, 0.0);
        int count = 0;
        while((std::norm(z1)<MAXZ) && (count<=NUMITR)) {
          std::complex<double> z = z1*z1+c+p*z2;
          z2 = z1;
          z1 = z;
          count++;
        }
        if(count < NUMITR)
          theRamCanvas.drawPoint(x, y, ct::csCCfractal0RYBCW::c(static_cast<ct::csIntType>(count*params[j][4])));
      }
    }
    theRamCanvas.writeTIFFfile("phoenix_" + mjr::math::str::fmt_int(j, 2, '0') + ".tiff");
    std::cout << "ITER(" << j <<  "): " << "DONE" << std::endl;
  }

  std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime;
  std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl;
}

Source Link: phoenix.cpp

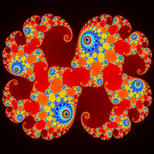
The above program will generate several images includeing this classic:

phoenix_00_10.png

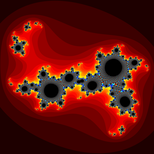
3. Static Image: Distance Estimator (Outside)

3.1. Code

#include "ramCanvas.hpp"

typedef mjr::ramCanvas3c8b::colorType ct;

std::vector<std::array<double, 9>> params {
  /*       cr,       ci,       pr,       pi,     k, x-min, x-max, y-min, y-max */
  {  0.566700,  0.00000, -0.50000,  0.00000, 100.0, -1.35,  1.35, -1.35,  1.35}, //  0 
  {  0.544992,  0.00000, -0.47000,  0.00000, 100.0, -1.35,  1.35, -1.35,  1.35}, //  1
  {  0.269000,  0.00000,  0.00000,  0.01000, 100.0, -1.10,  1.10, -1.00,  1.00}, //  2
  { -0.400000,  0.10000,  0.29550,  0.00000, 100.0, -1.10,  1.10, -1.50,  1.50}, //  3
  {  0.400000,  0.00000, -0.25000,  0.00000, 100.0, -1.30,  1.20, -1.00,  1.00}, //  4
};

int main(void) {
  std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now();
  const int    WIDTH  = 1920*1;
  const int    HEIGHT = 1920*1;
  const int    NUMITR = 500;
  const double MAXZ   = 4.0;

# pragma omp parallel for schedule(static,1)
  for(decltype(params.size()) j=0; j<params.size(); ++j) {
    const std::complex<double> c(params[j][0], params[j][1]);
    const std::complex<double> p(params[j][2], params[j][3]);
    mjr::ramCanvas3c8b theRamCanvas(WIDTH, HEIGHT, params[j][5], params[j][6], params[j][7], params[j][8]);
    for(int y=0;y<theRamCanvas.getNumPixY();y++) {
      for(int x=0;x<theRamCanvas.getNumPixX();x++) {
        std::complex<double> d1(1.0, 0.0);
        std::complex<double> d2(0.0, 0.0);

        std::complex<double> z1(theRamCanvas.int2realY(y), theRamCanvas.int2realX(x));
        std::complex<double> z2(0.0, 0.0);
        int count = 0;
        while((std::norm(z1)<MAXZ) && (count<=NUMITR)) {
          std::complex<double> z = z1*z1+c+p*z2;
          std::complex<double> d = 2.0*d1*z1+p*d2;
          z2 = z1;
          z1 = z;
          d2 = d1;
          d1 = d;
          count++;
        }
        if(count < NUMITR)
          theRamCanvas.drawPoint(x, y, ct::csCCfractal0RYBCW::c(static_cast<ct::csIntType>(std::log(std::abs(d1)+1)*params[j][4])));
      }
    }
    theRamCanvas.writeTIFFfile("phoenixD_" + mjr::math::str::fmt_int(j, 2, '0') + ".tiff");
    std::cout << "ITER(" << j <<  "): " << "DONE " << std::endl;
  }

  std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime;
  std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl;
}

Source Link: phoenixD.cpp

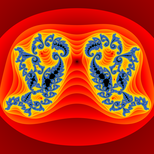
4. Static Image: Distance Estimator (Inside)

4.1. Code

#include "ramCanvas.hpp"

typedef mjr::ramCanvas3c8b::colorType ct;

std::vector<std::array<double, 9>> params {
  /*       cr,       ci,       pr,       pi,      k, x-min, x-max, y-min, y-max */
  {  0.566700,  0.00000, -0.50000,  0.00000,  300.0, -1.35,  1.35, -1.35,  1.35}, //  0 
  {  0.544992,  0.00000, -0.47000,  0.00000, 1000.0, -1.35,  1.35, -1.35,  1.35}, //  1
  { -0.400000,  0.10000,  0.29550,  0.00000,  300.0, -1.10,  1.10, -1.50,  1.50}, //  2
};

int main(void) {
  std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now();
  const int    WIDTH  = 1920*4*4;
  const int    HEIGHT = 1920*4*4;
  const int    NUMITR = 500;
  const double MAXZ   = 6.0;

# pragma omp parallel for schedule(static,1)
  for(decltype(params.size()) j=0; j<params.size(); ++j) {
    const std::complex<double> c(params[j][0], params[j][1]);
    const std::complex<double> p(params[j][2], params[j][3]);
    mjr::ramCanvas3c8b theRamCanvas(WIDTH, HEIGHT, params[j][5], params[j][6], params[j][7], params[j][8]);
    for(int y=0;y<theRamCanvas.getNumPixY();y++) {
      for(int x=0;x<theRamCanvas.getNumPixX();x++) {
        std::complex<double> d1(1.0, 0.0);
        std::complex<double> d2(0.0, 0.0);

        std::complex<double> z1(theRamCanvas.int2realY(y), theRamCanvas.int2realX(x));
        std::complex<double> z2(0.0, 0.0);
        int count = 0;
        while((std::norm(z1)<MAXZ) && (count<=NUMITR)) {
          std::complex<double> z = z1*z1+c+p*z2;
          std::complex<double> d = 2.0*d1*z1+p*d2;
          z2 = z1;
          z1 = z;
          d2 = d1;
          d1 = d;
          count++;
        }
        if(std::norm(z1)<MAXZ)
          theRamCanvas.drawPoint(x, y, ct::csCCfractal0RYBCW::c(static_cast<ct::csIntType>(std::log(std::abs(d1)+1)*params[j][4])));
      }
    }
    theRamCanvas.scaleDownMean(4);
    theRamCanvas.writeTIFFfile("phoenixI_" + mjr::math::str::fmt_int(j, 2, '0') + ".tiff");
    std::cout << "ITER(" << j <<  "): " << "DONE " << std::endl;
  }

  std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime;
  std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl;
}

Source Link: phoenixI.cpp

5. Making Movies

Becasue the phoenix has a couple free parameters, we can easily make movies by sweeping these parameters through a sequence of values.

5.1. Sweeping p

The following code will sweep \(p\) across a tiny range: 

#include "ramCanvas.hpp"

typedef mjr::ramCanvas3c8b::colorType ct;

int main(void) {
  std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now();
  const int    WIDTH  = 1920/2;
  const int    HEIGHT = 1920/2;
  const int    NUMITR = 500;
  const double MAXZ   = 4.0;

  const int    NUMFRM = 24*2;
  const double ANGMIN = 0.0;
  const double ANGMAX = std::numbers::pi*2;
  const double RADIUS = 0.0001;

# pragma omp parallel for schedule(static,1)
  for(int frame=0; frame<NUMFRM; frame++) {
#   pragma omp critical
    std::cout << "Frame: " << frame << std::endl;
    double angle = frame*(ANGMAX-ANGMIN)/NUMFRM+ANGMIN;

    const std::complex<double> c(0.566700, 0.00000);
    const std::complex<double> p(-0.50000+RADIUS*std::cos(angle),  0.00000);
    mjr::ramCanvas3c8b theRamCanvas(WIDTH, HEIGHT, -0.75, -0.5, 0.13, 0.32);

    for(int y=0;y<theRamCanvas.getNumPixY();y++) {
      for(int x=0;x<theRamCanvas.getNumPixX();x++) {
        std::complex<double> z1(theRamCanvas.int2realY(y), theRamCanvas.int2realX(x));
        std::complex<double> z2(0.0, 0.0);
        int count = 0;
        while((std::norm(z1)<MAXZ) && (count<=NUMITR)) {
          std::complex<double> z = z1*z1+c+p*z2;
          z2 = z1;
          z1 = z;
          count++;
        }
        if(count < NUMITR)
          theRamCanvas.drawPoint(x, y, ct::csCCfractal0RYBCW::c(static_cast<ct::csIntType>(count*10)));
      }
    }
    theRamCanvas.writeTIFFfile("phoenixM_" + mjr::math::str::fmt_int(frame, 2, '0') + ".tiff");
#   pragma omp critical
    std::cout << "FRAME(" << frame <<  "): " << "DONE" << std::endl;
  }

  std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime;
  std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl;
}

Source Link: phoenixM.cpp

The result is the following movie:

phoenixM.gif

5.2. Sweeping both c & p

The following code will sweep \(p\) and \c\) around tiny circles in the complex plane. 

#include "ramCanvas.hpp"

typedef mjr::ramCanvas3c8b::colorType ct;

int main(void) {
  std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now();
  const int    WIDTH  = 1920/2;
  const int    HEIGHT = 1920/2;
  const int    NUMITR = 40;
  const double MAXZ   = 4.0;

  const int    NUMFRM = 24*2;
  const double ANGMIN = 0.0;
  const double ANGMAX = std::numbers::pi*2;
  const double RADIUS = 0.06;

# pragma omp parallel for schedule(static,1)
  for(int frame=0; frame<NUMFRM; frame++) {
#   pragma omp critical
    std::cout << "Frame: " << frame << std::endl;
    double angle = frame*(ANGMAX-ANGMIN)/NUMFRM+ANGMIN;

    const std::complex<double> c(-0.400000+RADIUS*std::cos(angle),  0.10000+RADIUS*std::sin(angle));
    const std::complex<double> p(0.29550+RADIUS*std::cos(angle),  0.00000+RADIUS*std::sin(angle));
    mjr::ramCanvas3c8b theRamCanvas(WIDTH, HEIGHT, -1.10,  1.10, -1.50,  1.50);

    for(int y=0;y<theRamCanvas.getNumPixY();y++) {
      for(int x=0;x<theRamCanvas.getNumPixX();x++) {
        std::complex<double> z1(theRamCanvas.int2realY(y), theRamCanvas.int2realX(x));
        std::complex<double> z2(0.0, 0.0);
        int count = 0;
        while((std::norm(z1)<MAXZ) && (count<=NUMITR)) {
          std::complex<double> z = z1*z1+c+p*z2;
          z2 = z1;
          z1 = z;
          count++;
        }
        if ((count < NUMITR) && (count > 5))
          theRamCanvas.drawPoint(x, y, ct::csCCfractal0RYBCW::c(static_cast<ct::csIntType>(std::log(count)*110)));
      }
    }
    theRamCanvas.writeTIFFfile("phoenixM2_" + mjr::math::str::fmt_int(frame, 2, '0') + ".tiff");
#   pragma omp critical
    std::cout << "FRAME(" << frame <<  "): " << "DONE" << std::endl;
  }

  std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime;
  std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl;
}

Source Link: phoenixM.cpp

The result is the following movie:

phoenixM2.gif

6. References

  • S. Ushiki, "Phoenix" in IEEE Transactions on Circuits and Systems, vol. 35, no. 7, pp. 788-789, July 1988, doi: 10.1109/31.1825.

Check out the fractals section of my reading list.

All the code used to generate everything on this page may be found on github.