Mitch Richling: Hopalong Fractals
| Author: | Mitch Richling |
| Updated: | 2024-10-31 |
Table of Contents
1. Introduction
Barry Martin's "Hopalong" orbit fractals are a family of discrete-time dynamical systems:
- Classic Barry Martin fractal: \[ \begin{align*} x_{n+1} & = y_n - \mathrm{sgn}(x_n) \cdot \sqrt{\vert b x_n-c\vert} \\ y_{n+1} & = a-x_n \end{align*} \]
- Positive Barry Martin fractal: \[ \begin{align*} x_{n+1} & = y_n + \mathrm{sgn}(x_n) \cdot \sqrt{\vert b x_n-c\vert} \\ y_{n+1} & = a-x_n \end{align*} \]
- Additive Barry Martin fractal: \[ \begin{align*} x_{n+1} & = y_n + \sqrt{\vert b x_n-c\vert} \\ y_{n+1} & = a-x_n \end{align*} \]
- Sinusoidal Barry Martin fractal: \[ \begin{align*} x_{n+1} & = y_n + \sin{(b x_n-c)} \\ y_{n+1} & = a-x_n \end{align*} \]
All of these maps, and others, may be constructed from the following system as special cases: \[ \begin{align*} x_{n+1} & = y_n+d \cdot \mathrm{ssgn}(x_n) \cdot \left(f \cdot \sqrt{\vert b x_n-c\vert} + g \cdot \sin{(b x_n-c)} + h \cdot \vert b x_n-c\vert \right) \\ y_{n+1} & = a-x_n \end{align*} \] Where \[ \mathrm{ssgn}(v) = \cases{ s & $v\lt 0$ \cr 1 & $v\ge 0$ } \] \[ \mathrm{sgn}(v) = \cases{ -1 & $v\lt 0$ \cr +1 & $v\ge 0$ } \]
Note the simplified form of the \(\mathrm{sgn}(v)\) function used – the standard definition may be used for nearly identical results.
Some special cases:
- When \( d=-1, s=-1, f=1, g=0, h=0 \), the map becomes the "Classic Barry Martin fractal"
- When \( d=1, s=-1, f=1, g=0, h=0 \), the map becomes the "Positive Barry Martin fractal"
- When \( d=1, s=1, f=1, g=0, h=0 \), the map becomes the "Additive Barry Martin fractal"
- When \( d=1, s=1, f=0, g=1, h=0, c=0 \), the map becomes the "Sinusoidal Barry Martin fractal"
- When \( d=1, s=1, f=0, g=0, h=1, c=0 \), the map becomes the "The Gingerbread Man": \[ \begin{align*} x_{n+1} & = y_n + \sin{(b x_n)} \\ y_{n+1} & = a-x_n \end{align*} \]
- When \( d=1, s=1, f=0, g=0, h=1, c\ne0 \), the map becomes the "The Shifted Gingerbread Man": \[ \begin{align*} x_{n+1} & = y_n + \sin{(b x_n-c)} \\ y_{n+1} & = a-x_n \end{align*} \]
2. Algorithms
Just as with the Peter de Jong attractors we look at the probability density function, \(P(x,y)\), defined by the probability that some \((x_n, y_n)\) from the map will be in a neighborhood of \((x,y)\). While that sounds complicated, producing a visualization of this PDF is quite simple in practice – we simply visualize a histogram based on computed values of the map. The first step is to define a rectangular region of the plane over which we wish to visualize the PDF, and then define a set of discrete pixels over that region. Then we compute a few million, or billion, iterations of the map, and count the number of times we hit each pixel.
#include "ramCanvas.hpp" std::vector<std::array<double, 14>> params { /* a b c d, s, f, g, h, n, k, x-min, x-max, y-min, y-max */ { -2.00000, -0.33000, 0.01000, -1.0, -1.0, 1.0, 0.0, 0.0, 4.0e7, 1.0, -18.0, 17.0, -18.0, 17.0}, // 0 { 0.40000, 1.10000, 0.00000, -1.0, -1.0, 1.0, 0.0, 0.0, 2.5e7, 1.0, -7.0, 7.0, -7.0, 7.0}, // 1 { -3.14000, 0.20000, 0.30000, -1.0, -1.0, 1.0, 0.0, 0.0, 3.0e7, 1.0, -40.0, 40.0, -40.0, 40.0}, // 2 { -3.14000, 0.19000, 0.32000, 1.0, -1.0, 1.0, 0.0, 0.0, 1.0e7, 1.0, -38.0, 35.0, -38.0, 35.0}, // 3 { -2.14000, -0.20000, 0.30000, 1.0, 1.0, 1.0, 0.0, 0.0, 3.0e7, 0.5, -9.0, 7.0, -9.0, 7.0}, // 4 { 0.40000, 1.00000, 0.00000, -1.0, -1.0, 0.0, 1.0, 0.0, 2.0e6, 1.0, -70.0, 70.0, -70.0, 70.0}, // 5 { -3.14000, 0.20000, 0.30000, -1.0, -1.0, 0.0, 1.0, 0.0, 6.0e7, 1.0, -45.0, 45.0, -45.0, 45.0}, // 6 { -3.14000, 0.20000, 0.30000, 1.0, -1.0, 0.0, 1.0, 0.0, 1.0e7, 1.0, -35.0, 35.0, -35.0, 35.0}, // 7 { -2.00000, -0.33000, 0.01000, -1.0, -1.0, 1.0, 0.0, 1.0, 4.0e7, 1.0, -25.0, 25.0, -25.0, 25.0}, // 8 { -3.14000, 0.20000, 0.30000, -1.0, -1.0, 1.0, 0.0, 1.0, 4.0e7, 1.0, -60.0, 60.0, -60.0, 60.0}, // 9 { -3.14000, 0.20000, 0.30000, 1.0, -1.0, 1.0, 0.0, 1.0, 6.0e7, 1.0, -90.0, 90.0, -90.0, 90.0}, // 10 { -3.14000, 0.20000, 0.30000, -1.0, -1.0, 0.0, 0.0, 1.0, 2.0e7, 1.0, -17.0, 15.0, -17.0, 15.0}, // 11 { -3.14000, 0.20000, 0.30000, 1.0, -1.0, 0.0, 0.0, 1.0, 3.0e7, 1.0, -17.0, 14.0, -17.0, 14.0}, // 12 { -3.14000, 0.20000, 0.30000, 1.0, -1.0, 0.0, 0.0, 1.0, 1.0e7, 1.0, -17.0, 14.0, -17.0, 14.0}, // 13 { -1.14000, 0.01000, 0.05000, 1.0, -1.0, 0.0, 0.0, 1.0, 5.0e6, 1.0, -3.5, 2.5, -3.5, 2.5}, // 14 { -1.14000, 0.10000, 0.50000, 1.0, -1.0, 0.0, 0.0, 1.0, 6.0e7, 1.0, -17.0, 14.0, -17.0, 14.0}, // 15 }; int main(void) { std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now(); const int BSIZ = 480*8; mjr::ramCanvas1c16b::colorType aColor; aColor.setChans(1); for(decltype(params.size()) j=0; j<params.size(); ++j) { mjr::ramCanvas1c16b theRamCanvas(BSIZ, BSIZ, params[j][10], params[j][11], params[j][12], params[j][13]); double a = params[j][0]; double b = params[j][1]; double c = params[j][2]; double d = params[j][3]; double s = params[j][4]; double k = params[j][9]; double f = params[j][5]; double g = params[j][6]; double h = params[j][7]; /* Draw the Attractor on a 16-bit, greyscale canvas such that the level is the hit count for that pixel. Thus we are using an "image" as a way to store field data instead of color information. */ double x = 0.0; double y = 0.0; uint64_t maxII = 0; uint64_t inCnt = 0; uint64_t maxItr = static_cast<uint64_t>(params[j][8]); uint64_t iPrt = maxItr / 5; for(uint64_t i=1;i<maxItr;i++) { double xNew = y+d*(x<0.0?s:1.0)* (f*std::sqrt(std::abs(b*x-c)) + g*std::sin(b*x-c) + h*std::abs(b*x-c)); double yNew = a-x; if ( !theRamCanvas.isCliped(x, y)) { inCnt++; theRamCanvas.drawPoint(x, y, theRamCanvas.getPxColor(x, y).tfrmAdd(aColor)); if(theRamCanvas.getPxColor(x, y).getC0() > maxII) { maxII = theRamCanvas.getPxColor(x, y).getC0(); if(maxII > 16384) { // 1/4 of max possible intensity std::cout << "ITER(" << j << "): " << i << " MAXS: " << maxII << " EXIT: Maximum image intensity reached" << std::endl; break; } } } if((i % iPrt) == 0) std::cout << "ITER(" << j << "): " << i << " MAXS: " << maxII << " INC: " << inCnt << std::endl; x=xNew; y=yNew; } std::cout << "ITER(" << j << "): " << "DONE" << " MAXS: " << maxII << " INC: " << inCnt << std::endl; // Log image transform theRamCanvas.applyHomoPixTfrm(&mjr::ramCanvas1c16b::colorType::tfrmLn1); maxII = static_cast<uint64_t>(std::log(static_cast<double>(maxII))); /* Create a new image based on csCCfractal0RYBCW -- this one is 24-bit RGB color. */ mjr::ramCanvas3c8b anotherRamCanvas(BSIZ, BSIZ); typedef mjr::ramCanvas3c8b::colorType::csCCfractal0RYBCW cs_t; for(int yi=0;yi<theRamCanvas.getNumPixY();yi++) for(int xi=0;xi<theRamCanvas.getNumPixX();xi++) anotherRamCanvas.drawPoint(xi, yi, cs_t::c(k * theRamCanvas.getPxColor(xi, yi).getC0() / static_cast<mjr::ramCanvas3c8b::csFltType>(maxII))); anotherRamCanvas.writeTIFFfile("barrymartin_" + mjr::math::str::fmt_int(j, 2, '0') + ".tiff"); } std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime; std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl; return 0; }
Source Link: barrymartin.cpp
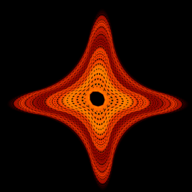
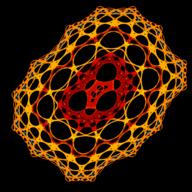
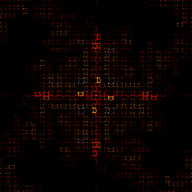
The above program will generate several images includeing the "Classic Barry Martin Atractor":
4. References
- Martin, Barry. 1989. "Graphic Potential of Recursive Functions." In Computers in Art, Design and Animation, 109-29. Berlin, Heidelberg: Springer-Verlag.
- A. K. Dewdney. 1986. "Wallpaper for the Mind: Computer Images That Are Almost, but Not Quite, Repetitive." Scientific American, September, 12-23.
Check out the fractals section of my reading list.
All the code used to generate everything on this page may be found on github.