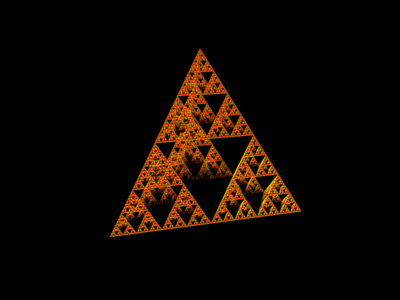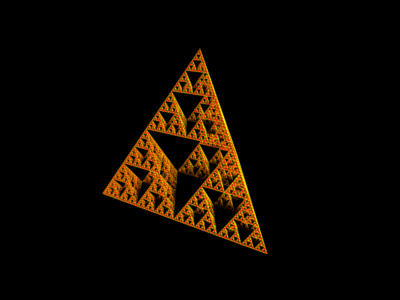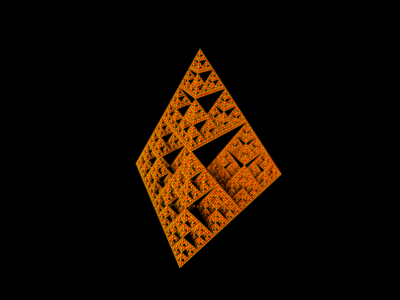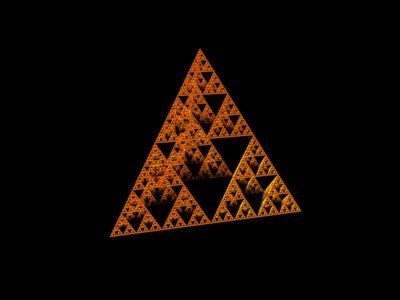Mitch Richling: Sierpinski Sponge (3D Gasket)

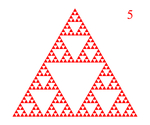
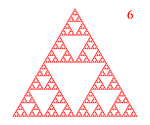
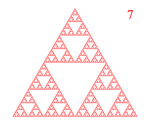
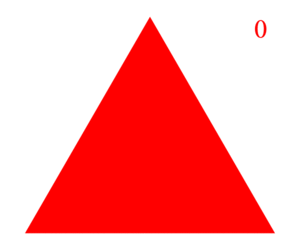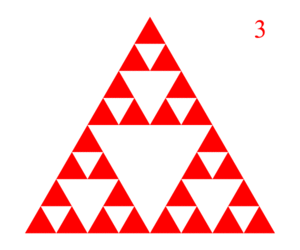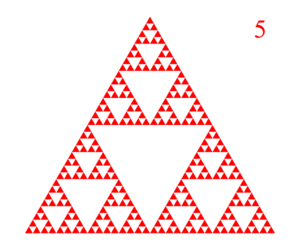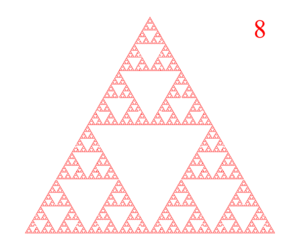
The Sierpinski gasket is a subset of the Euclidean plane resulting from an infinite sequence of operations with triangles. We begin the construction of the Sierpinski gasket with a single equilateral triangle. Then we remove from its center the largest equilateral triangle we can. This process is repeated with each remaining triangle. The first 9 steps are illustrated below:

Just for fun, here is an animation of the process:

The result of continuing this process forever is the Sierpinski gasket. Infinite constructions like this lead to some surprising results. For example, the area of the Sierpinski gasket is zero while it perimeter is infinite! While we can't capture the infinite complexity of the Sierpinski gasket on a finite computer display, we can still create some pretty cool images – especially when we move to 3D!.

The two dimensional process leading to the Sierpinski gasket can be generalized into the 3rd dimension. Instead of beginning with a triangle, we start with a regular tetrahedron. Then we remove the maximal, inverted tetrahedron from the center. Next, we continue this process by removing the centers of the remaining tetrahedra in a similar way. Continue this process forever, and the result if the 3D Sierpinski sponge. The first few iterations of this process are illustrated here:

Click on the above thumbnails in order to access MOVIES of the object as well as alternative views with a dark background

These objects are not easy to render. The result of iterating the process only 8 times yields an 82MB Povray input file containing more than half a million geometric primitives! Rendered with 5 light sources and with high quality settings, Povray takes about half an hour even on fast hardware circa 2014.

Check out the fractals section of my reading list.