Mitch Richling: Symmetric Fractals
| Author: | Mitch Richling |
| Updated: | 2022-10-05 |
Table of Contents
1. Symmetric Fractals
The symmetric fractals featured on this page were inspired by the book "Symmetry in Chaos" by Michael Field and Martin Golubitsky. All of the fractals here are generated from the same equation:
\[z_{k+1} = (\lambda + \alpha z_k \overline{z_k} + \beta\, \Re(z_k^n) + \omega i) z_k + \gamma \overline{z_k}^{(n-1)}\]
Where the following are constants (n is an integer and the rest are real):
\[\lambda\,\, \alpha\,\, \beta\,\, \omega\,\, \gamma\,\, n\]
and the iteration begins with:
\[z_0 = \frac{1}{100} + \frac{1}{100} i \]
Just as with the Peter de Jong attractors we look at the probably density function, \(P(x,y)\), defined by the probably that some \((x_n, y_n)\) from the map will be in a neighborhood of \((x,y)\). While that sounds complicated, producing a visualization of this PDF is quite simple in practice – we simply visualize a histogram based on computed values of the map. The first step is to define a rectangular region of the plane over which we wish to visualize the PDF, and then define a set of discrete pixels over that region. Then we compute a few million, or billion, iterations of the map, and count the number of times we hit each pixel.
2. Code: Drawing Things
Some code will make the above discussion clear:
#include "ramCanvas.hpp" typedef mjr::ramCanvas3c8b rct; typedef rct::colorType ct; const int NPR = 27; typename mjr::ramCanvas1c16b::coordFltType params[NPR][12] = { /* lambda alpha beta gamma omega n ipw xmin xmax ymin ymax 1=mean */ { 1.375390, -0.4212800, 0.26969, 0.08352, 0.338347, 6, 15.00, -1.30, 1.30, -1.30, 1.30, 1.0}, // 0 | { 1.600230, -1.1340800, -0.17506, 0.67872, 0.049490, 6, 14.00, 0.10, 0.70, 0.43, 0.90, 0.0}, // 1 | WACKY { 1.000890, -0.7678100, 1.89425, -1.13943, -0.688827, 7, 10.00, -0.90, 0.90, -0.90, 0.90, 0.0}, // 2 | {-1.563400, 1.7238200, 0.74440, 0.71874, 0.258907, 3, 8.00, -0.75, 0.75, -0.75, 0.75, 1.0}, // 3 | { 1.361000, -1.8225400, -0.92635, -1.74108, -0.761120, 5, 2.00, -0.70, 0.70, -0.70, 0.70, 1.0}, // 4 | { 1.609310, -1.6924900, 0.85055, 0.26523, -0.716769, 5, 4.00, -0.90, 0.90, -0.90, 0.90, 0.0}, // 5 | { 1.464900, -1.8825700, -1.47205, -0.83559, -0.701477, 4, 3.00, -0.80, 0.80, -0.80, 0.80, 1.0}, // 6 | { 1.622110, -1.0694500, -0.11181, 0.62253, 0.784032, 4, 2.00, -1.20, 1.20, -1.20, 1.20, 1.0}, // 7 | {-1.380150, 0.7472100, 1.17094, 0.05782, -0.574188, 6, 10.00, -1.00, 1.00, -1.00, 1.00, 0.0}, // 8 | { 0.335010, -1.3467500, -0.65137, -0.87848, -1.231490, 5, 10.00, -1.20, 1.20, -1.20, 1.20, 1.0}, // 9 | {-1.496290, 1.8701600, -1.93938, -0.88084, -0.139602, 3, 10.00, -0.55, 0.55, -0.55, 0.55, 1.0}, // 10 | {-1.248610, 1.0816100, -0.50731, 0.97272, -0.853955, 11, 10.00, -1.00, 1.00, -1.00, 1.00, 0.0}, // 11 | {-1.991900, 1.8219100, -0.38273, 0.68143, 0.493416, 11, 10.00, -1.00, 1.00, -1.00, 1.00, 0.0}, // 12 | { 1.694170, -1.2730200, 0.75035, -1.28615, 0.561096, 6, 2.50, -1.10, 1.10, -1.10, 1.10, 1.0}, // 13 | {-0.386753, -0.0610025, -1.02847, 0.78619, -0.984828, 3, 5.00, -1.20, 1.20, -1.20, 1.20, 0.0}, // 14 | special { 0.982876, -1.1125600, 0.500411, -1.44111, -1.008560, 4, 7.00, -0.80, 0.80, -0.80, 0.80, 0.0}, // 15 | special {-1.257170, 0.0390811, 0.13892, -0.87058, 0.023977, 7, 2.60, -1.20, 1.20, -1.20, 1.20, 1.0}, // 16 | Neat { 1.008500, 0.2275230, -0.56604, -0.62146, 0.693161, 5, 3.00, -1.20, 1.20, -1.20, 1.20, 1.0}, // 17 | { 1.618250, -1.6035300, 1.13920, -1.60120, -0.761638, 5, 2.80, -1.00, 1.00, -1.00, 1.00, 0.0}, // 18 | {-0.960670, 0.0834029, 1.01438, 1.05748, -0.599590, 21, 2.60, -1.20, 1.20, -1.20, 1.20, 1.0}, // 19 | { 0.908230, 0.3047990, 1.03560, 0.29872, -0.473521, 7, 3.00, -1.20, 1.20, -1.20, 1.20, 0.0}, // 20 | { 1.873130, -1.2822600, -1.28938, -1.36355, -0.141951, 21, 2.00, -1.10, 1.10, -1.10, 1.10, 1.0}, // 21 | NICE { 1.536250, -0.6547000, -1.43255, -0.24270, 0.128769, 31, 2.50, -1.00, 1.00, -1.00, 1.00, 0.0}, // 22 | NICE {-2.080000, 1.0000000, -0.10000, 0.16700, 0.000000, 7, 4.00, -1.20, 1.20, -1.20, 1.20, 0.0}, // 23 | d7 SIC BOOK {-2.500000, 5.0000000, -1.90000, 1.00000, 0.180000, 5, 2.75, -0.75, 0.75, -0.75, 0.75, 0.0}, // 24 | Z5 SIC BOOK { 2.500000, -2.5000000, 0.00000, 0.90000, 0.000000, 3, 2.75, -1.40, 1.40, -1.40, 1.40, 0.0}, // 25 | D3 SIC BOOK { 2.600000, -2.0000000, 0.00000, -0.50000, 0.000000, 5, 4.75, -1.30, 1.30, -1.30, 1.30, 1.0}, // 26 | D5 SIC BOOK }; // This is *identical* to what we did in pickoverPopcorn.cpp -- just way shorter. It is longer still because we don't make // this a subclass of ramCanvasTpl::rcConverterHomoBase in order to illustrate how to implement a RC converter from scratch. // Also note we didn't need to DIY the color gradient with cmpRGBcornerDGradiant() as this gradient (0RYBCW) is available as // a pre-built color scheme: csCCfractal0RYBCW. class g2rgb8 { private: mjr::ramCanvas1c16b& attachedRC; int factor; public: g2rgb8(mjr::ramCanvas1c16b& aRC, uint64_t newFactor) : attachedRC(aRC), factor(static_cast<int>(newFactor)) { } inline bool isIntAxOrientationNaturalX() { return attachedRC.isIntAxOrientationNaturalX(); } inline bool isIntAxOrientationNaturalY() { return attachedRC.isIntAxOrientationNaturalY(); } inline mjr::ramCanvas1c16b::coordIntType getNumPixX() { return attachedRC.getNumPixX(); } inline mjr::ramCanvas1c16b::coordIntType getNumPixY() { return attachedRC.getNumPixY(); } typedef mjr::colorRGB8b colorType; inline colorType getPxColorNC(rct::coordIntType x, rct::coordIntType y) { colorType retColor; rct::csIntType tmp = static_cast<rct::csIntType>(attachedRC.getPxColorNC(x, y).getC0() * 1275 / factor); return retColor.cmpRGBcornerDGradiant(tmp, "0RYBCW"); } }; int main(void) { std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now(); const int BSIZ = 7680/4; mjr::ramCanvas1c16b::colorType aColor; aColor.setChans(1); //for(int j=0; j<NPR; j++) { for(int j : { 0 } ) { mjr::ramCanvas1c16b theRamCanvas(BSIZ, BSIZ, params[j][7], params[j][8], params[j][9], params[j][10]); typename mjr::ramCanvas1c16b::coordFltType lambda = params[j][0]; typename mjr::ramCanvas1c16b::coordFltType alpha = params[j][1]; typename mjr::ramCanvas1c16b::coordFltType beta = params[j][2]; typename mjr::ramCanvas1c16b::coordFltType gamma = params[j][3]; typename mjr::ramCanvas1c16b::coordFltType w = params[j][4]; double ipw = static_cast<double>(params[j][6]); int n = static_cast<int>( params[j][5]); int filter = static_cast<int>( params[j][11]); std::complex<typename mjr::ramCanvas1c16b::coordFltType> cplxi (0,1); uint64_t maxitr = 10000000000ul; std::complex<typename mjr::ramCanvas1c16b::coordFltType> z(.01,.01); uint64_t maxII = 0; for(uint64_t i=0;i<maxitr;i++) { z = (lambda + alpha*z*std::conj(z)+beta*std::pow(z, n).real() + w*cplxi)*z+gamma*std::pow(std::conj(z), n-1); typename mjr::ramCanvas1c16b::coordFltType x=z.real(), y=z.imag(); if(i>1000) theRamCanvas.drawPoint(x, y, theRamCanvas.getPxColor(x, y).tfrmAdd(aColor)); if(theRamCanvas.getPxColor(x, y).getC0() > maxII) { maxII = theRamCanvas.getPxColor(x, y).getC0(); if(maxII > 16384) { // 1/4 of max possible intensity std::cout << "ITER(" << j << "): " << i << " MAXS: " << maxII << " EXIT: Maximum image intensity reached" << std::endl; break; } } if((i % 10000000) == 0) std::cout << "ITER(" << j << "): " << i << " MAXS: " << maxII << std::endl; } std::cout << "ITER(" << j << "): " << "Big TIFF" << std::endl; theRamCanvas.writeTIFFfile("sic_" + std::to_string(j) + ".tiff"); // Root image transform std::cout << "ITER(" << j << "): " << "TFRM & SCALE" << std::endl; theRamCanvas.autoHistStrech(); //theRamCanvas.applyHomoPixTfrm(&mjr::ramCanvas1c16b::colorType::tfrmLn); theRamCanvas.applyHomoPixTfrm(&mjr::ramCanvas1c16b::colorType::tfrmStdPow, 1/ipw); if(filter) theRamCanvas.scaleDownMean(4); else theRamCanvas.scaleDownMax(4); theRamCanvas.autoHistStrech(); // Compte new image max intensity std::cout << "ITER(" << j << "): " << "MAX" << std::endl; maxII = 0; for(auto& pixel : theRamCanvas) if(pixel.getC0() > maxII) maxII = pixel.getC0(); std::cout << "ITER(" << j << "): " << "TIFF" << std::endl; /* Dump the 16-bit grayscale TIFF */ theRamCanvas.writeTIFFfile("sicM_" + std::to_string(j) + ".tiff"); /* Now we would like a false color version (24-bit RGB). We could create a new canvas like this: rct cRamCanvas(theRamCanvas.getNumPixX(), theRamCanvas.getNumPixY()); for(mjr::ramCanvas1c16b::coordIntType y=0;y<theRamCanvas.getNumPixY();y++) for(mjr::ramCanvas1c16b::coordIntType x=0;x<theRamCanvas.getNumPixX();x++) { auto ci = static_cast<rct::csIntType>(theRamCanvas.getPxColorRefNC(x, y).getC0() * 1275 / maxII) cRamCanvas.getPxColorRefNC(x, y).cmpRGBcornerDGradiant(ci, "0RYBCW"); } cRamCanvas.writeTIFFfile("sicC_" + std::to_string(j) + ".tiff"); We have a better way. One that dosen't require the RAM to create a brand new canvas. We can use the filter option of writeTIFFfile! */ g2rgb8 rcFilt(theRamCanvas, maxII); theRamCanvas.writeTIFFfile("sicCC_" + std::to_string(j) + ".tiff", rcFilt, false); } std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime; std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl; return 0; }
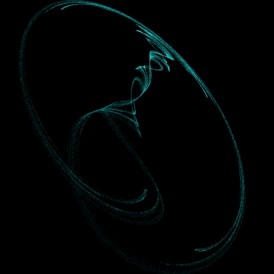
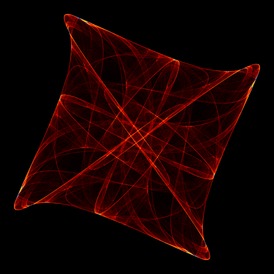
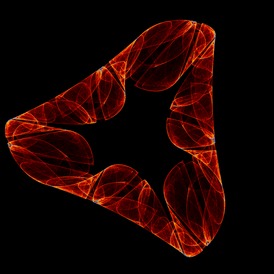
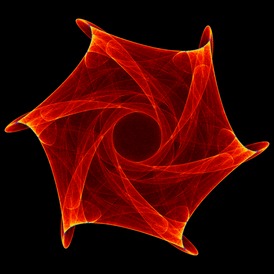
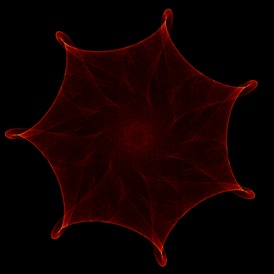
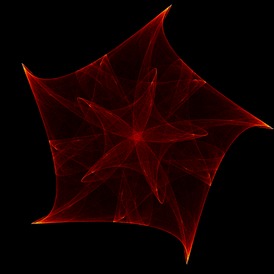
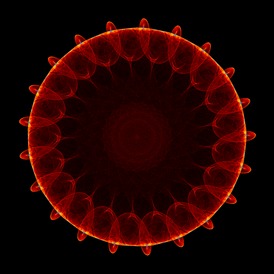
3. Gallery
Here are a few examples. Most of these were discovered via an automated search program using the technique briefly outlined in the next section. When you draw one of these images with a random set of parameters, the odds are that you are the first human being ever to see that precise image – with five, 32-bit parameters the odds of someone else picking the same parameters is 1 in 2^160.
4. Code: Finding Things
The following code will help to find interesting candidates for parameters:
#include "ramCanvas.hpp" int main(void) { std::chrono::time_point<std::chrono::system_clock> startTime = std::chrono::system_clock::now(); const int BSIZ = 2048; std::random_device rd; std::mt19937 rEng(rd()); std::uniform_real_distribution<double> uniform_dist_double(-2.0, 2.0); std::uniform_int_distribution<int> uniform_dist_int(3, 7); mjr::ramCanvas1c16b theRamCanvas(BSIZ, BSIZ, -2, 2, -2, 2); // Just used for coordinate conversion. ;) uint64_t maxCnt = 0; for(int j=0; j<100000; j++) { std::map<uint64_t, uint64_t> ptcnt; double lambda = uniform_dist_double(rEng); double alpha = uniform_dist_double(rEng); double beta = uniform_dist_double(rEng); double gamma = uniform_dist_double(rEng); double w = uniform_dist_double(rEng); int n = uniform_dist_int(rEng); std::complex<double> z(0.01,0.01); for(uint64_t i=0;i<1000;i++) { z = (lambda + alpha*z*std::conj(z)+beta* std::pow(z, n).real() + w*std::complex<double>(0,1))*z+gamma*static_cast<std::complex<double>>(std::pow(std::conj(z), n-1)); ptcnt[((uint64_t)theRamCanvas.real2intX(z.real()))<<32 | ((uint64_t)theRamCanvas.real2intY(z.imag()))] = 1; } if(ptcnt.size() > maxCnt) { maxCnt = ptcnt.size(); std::cout << j << " " << maxCnt << " " << lambda << "," << alpha << "," << beta << "," << gamma << "," << w << "," << n << std::endl; } } std::chrono::duration<double> runTime = std::chrono::system_clock::now() - startTime; std::cout << "Total Runtime " << runTime.count() << " sec" << std::endl; return 0; }
5. Some Fine Points
This fractal system presents most of the same practical problems we encountered with the Peter de Jong attractors but with a few extra wrinkles:
- The image processing pipeline is both more sophisticated, and varies for each set of parameters.
- We can't always start with a fixed region of the plane, so this too varies with each set of parameters.
- More hand work is required when evaluating the results of automated parameter searching – the highest number of turned on pixels may not be the most interesting image..