Mitch Richling: Mitch Richling: Wada Basins From Three Mirrored Spheres

Author:	Mitch Richling
Updated:	2021-05-22

1. Introduction
2. Examples
3. References

1. Introduction

Mirrors are fun, and mirrors that aren't flat are the most fun of all. You do remember roasting ants in the back yard with Mom's makeup mirror when you were a kid? Right?!? This page is about the mathematical simulation of four spherical mirrors, and the fascinating, fantastically complex reflection patterns they produce. Ray-tracing programs are designed to simulate all sorts of optical effects including reflection, and so we will be using the open source ray-tracing package POV-Ray to simulate our mirrors…. First, we need to get a handle on the geometry of the situation.

Take four spheres of the same radius, and place them so that each sphere touches the other three spheres like so:

Note that the centers of the spheres are at the vertexes of a regular tetrahedron, that is a regular, triangular pyramid in the language of high school geometry. Next, place faces on three of the gaps like so:

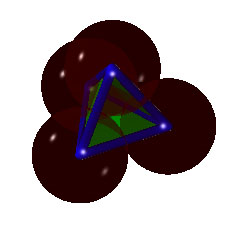
For our experiments below, the balls are all perfect mirrors. With our mirror finish balls correctly placed, we are ready to begin our tour of the many wonders of mirrors. Click on the images to view a larger, 800x600, version.

2. Examples

In this section, we start out simple and continue to the complex. First we simply build the necessary structure, and then we play with it a bit.

2.1. The simplest case – three balls

For our first image, lets color the faces of the tetrahedron red, green, and blue. We will look straight into the gap formed between the three front most spheres.

2.2. A bit more complex – add a tetrahedron

That was nice, now lets fill in that last face of the tetrahedron with a yellow triangle, and put the camera inside of the gap.

2.3. More reflections

Hmmmm. One would expect more reflections than what we are seeing. The answer is to bump up POV-Ray's max_trace_level parameter to a higher value. For the rest of our experiments, we will use a value of 16. This parameter controls the number of bounces a light ray can take before it is considered done. The image above becomes rather striking now.

If this is taken to the theoretical extreme, then one can prove mathematically that every epsilon ball contains a point of each color. I'll bet you didn't expect me to throw in that little bit of mathematics :) This kind of thing is known as a "Wada basin". Very kool stuff.

2.4. Beyond primary colors – GOLD!

Color is good, but what happens if we make the triangles have a gold finish?

2.5. What about monochrome?

Gold is KOOL! What happens if we make them white?

2.6. A different perspective

That is enough of looking at the back most sphere. Lets move our camera near the back most sphere, and point it at the front most triangle.

2.7. Now with gold

Very nice. Now lets try it with a gold texture.

2.8. Lets take a step back

Wow! That's quite a bit of complexity inside. Lets take a step back and see what we get from further away:

2.9. A bit more to reflect

I don't care for the lack of color on the spheres, and I really don't care for that black triangle in the middle. How can we add some color? Well the spheres are all mirrors! Give them something to reflect. Let's place a gold plane about 50 units away from the whole thing, behind the camera.

2.10. What about white?

How about a white plane.

2.11. And a littel closer

Let's increase the contrast by moving the plane in closer to the objects.

3. References

Check out the fractals section of my reading list.